এক্সেলে আইআরআর (IRR) ফাংশন সম্পর্কে জানতে গল্পটি শোনা যাক! রাজা নামের এক ব্যক্তি একটি ব্যবসা শুরু করার কথা ভাবছেন। ব্যবসাটি শুরু করতে তার ৭০,০০০ টাকা খরচ করতে হবে। তিনি আশা করছেন যে, ব্যবসাটি ভালো চলবে এবং প্রতি বছর লাভ হবে। তিনি আগামী পাঁচ বছরে কী পরিমাণ লাভ আশা করতে পারেন, সেটা বুঝতে চান।
এখানে এক্সেলের আইআরআর ফাংশন রাজাকে সাহায্য করতে পারে। আইআরআর ফাংশন হলো এমন একটা ফাংশন, যা একটা সিরিজের নগদ আয়-ব্যয়ের হিসাব করে ভবিষ্যতের মুনাফার হার বের করে দেয়।
আইআরআর ফাংশন কীভাবে কাজ করে?
আইআরআর ফাংশনের জন্য, রাজাকে তার নগদ আয়-व्यয়ের তথ্য এক্সেলে লিখতে হবে। এই তথ্যটিতে ব্যবসা শুরু করার খরচ (৭০,০০০ টাকা, নেতিবাচক মান) এবং প্রতি বছরের আয় (১২,০০০ টাকা, ১৫,০০০ টাকা, ১৮,০০০ টাকা, ২১,০০০ টাকা, এবং ২৬,০০০ টাকা) থাকবে।
আইআরআর ফাংশন এই তথ্যটি বিশ্লেষণ করে, এমন একটা আগ্রহের হার খুঁজে বের করে, যেখানে পাঁচ বছরের শেষে বর্তমান মূল্যে সব নগদ আয়- ব্যয় হিসাব মিলিয়ে যায় (মানে হয় শূন্য)।
আইআরআর ফাংশন ব্যবহারের নিয়ম:
- আপনাকে সেই সেলগুলোর রেঞ্জ দিতে হবে যেখানে আপনার নগদ আয়-व्यয়ের তথ্য আছে।
- ঐচ্ছিকভাবে, আপনি আইআরআর এর প্রাথমিক অনুমানও দিতে পারেন (যেমন, ১০%)। এটা ফাংশনকে হিসাব করতে সাহায্য করে।
আইআরআর ফাংশন ব্যবহারের উদাহরণ:
রাজা তার এক্সেল শিটে নিচের তথ্য লিখেছেন:
- সেল A1: বছর (১, ২, ৩, ৪, ৫)
- সেল B1: নগদ প্রবাহ (-৭০,০০০, ১২,০০০, ১৫,০০০, ১৮,০০০, ২৬,০০০)
সেল C1 এ, রাজা নিম্নলিখিত সূত্র লিখেছেন:
=IRR(B1:B6)Enter চাপার পর, সেল C1 -০.০২১ এর মান দেখাবে।
ফলাফলের ব্যাখ্যা:
-০.০২১ হলো মুনাফার হার (IRR)। এই মানটি ঋণাত্মক কারণ ব্যবসাটি শুরুতেই টাকা খরচ করিয়েছে (৭০,০০০ টাকা)।
- সহজ কথায়, -০.০২১ বা -২.১% হিসাব করে, রাজা তার ব্যবসায় প্রতি বছরে গড়ে ২.১% এর বেশি লাভ করতে পারবেন না, যাতে পাঁচ বছর পরে সব খরচ ও লাভের মিল হয়।
Description
Returns the internal rate of return for a series of cash flows represented by the numbers in values. These cash flows do not have to be even, as they would be for an annuity. However, the cash flows must occur at regular intervals, such as monthly or annually. The internal rate of return is the interest rate received for an investment consisting of payments (negative values) and income (positive values) that occur at regular periods.
Syntax
IRR(values, [guess])
The IRR function syntax has the following arguments:
- Values Required. An array or a reference to cells that contain numbers for which you want to calculate the internal rate of return.
- Values must contain at least one positive value and one negative value to calculate the internal rate of return.
- IRR uses the order of values to interpret the order of cash flows. Be sure to enter your payment and income values in the sequence you want.
- If an array or reference argument contains text, logical values, or empty cells, those values are ignored.
- Guess Optional. A number that you guess is close to the result of IRR.
- Microsoft Excel uses an iterative technique for calculating IRR. Starting with guess, IRR cycles through the calculation until the result is accurate within 0.00001 percent. If IRR can’t find a result that works after 20 tries, the #NUM! error value is returned.
- In most cases you do not need to provide guess for the IRR calculation. If guess is omitted, it is assumed to be 0.1 (10 percent).
- If IRR gives the #NUM! error value, or if the result is not close to what you expected, try again with a different value for guess.
Remarks
IRR is closely related to NPV, the net present value function. The rate of return calculated by IRR is the interest rate corresponding to a 0 (zero) net present value. The following formula demonstrates how NPV and IRR are related:
NPV(IRR(A2:A7),A2:A7) equals 1.79E-09 [Within the accuracy of the IRR calculation, the value is effectively 0 (zero).]
Example
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
| Data | Description | |
| -$70,000 | Initial cost of a business | |
| $12,000 | Net income for the first year | |
| $15,000 | Net income for the second year | |
| $18,000 | Net income for the third year | |
| $21,000 | Net income for the fourth year | |
| $26,000 | Net income for the fifth year | |
| Formula | Description | Result |
| =IRR(A2:A6) | Investment’s internal rate of return after four years | -2.1% |
| =IRR(A2:A7) | Internal rate of return after five years | 8.7% |
| =IRR(A2:A4,-10%) | To calculate the internal rate of return after two years, you need to include a guess (in this example, -10%). | -44.4% |
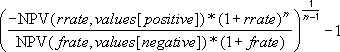
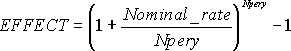
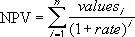
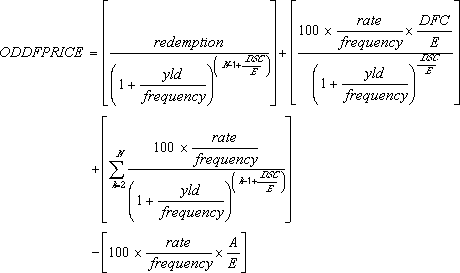 where:
where:
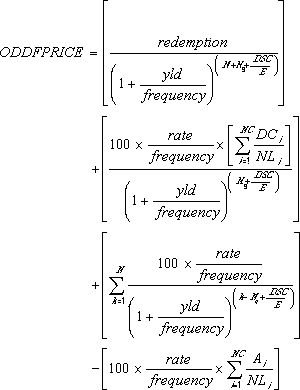 where:
where: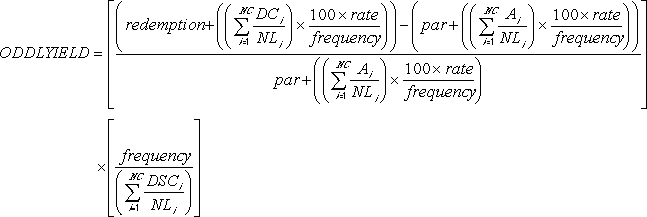 where:
where: